Answer:
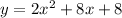
Explanation:
Notice that we are looking for a quadratic function that has only one real solution for y=0, that is a unique point that touches the x-axis
We need therefore to look at the discriminant associated with all 4 equations constructed by equaling y to zero. We then try to find one that gives discriminant zero , corresponding to a unique real solution to the equation.
a)
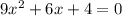 has discriminant:
has discriminant:
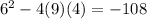
b)
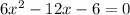 has discriminant:
has discriminant:
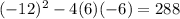
c)
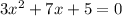 has discriminant:
has discriminant:
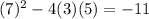
d)
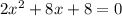 has discriminant:
has discriminant:
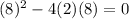
Therefore, the last function is the one that can have such graph