Answer:
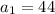
Explanation:
Recall the direct formula for an arithmetic sequence:
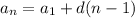
Where d is the common difference.
Therefore, we can write the following two equations:
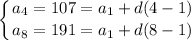
Solve the system. Simplifying yields:
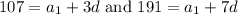
Subtracting the two equations into each other yields:
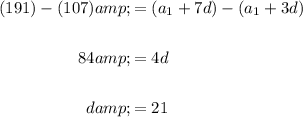
Using either equation, solve for the initial term:
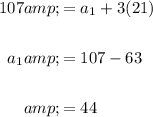
In conclusion, the initial term is 44.