Question

Log base 32 of 2
Help

Answer 1

`log_(32)(2)=0.2`

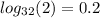
Explanation:

Recall that the unknown (x) here is the log base 32 of 2, so we can write this as the equation:

`log_(32)(2)=x`

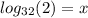
The above equation can be solved by the "change of base formula":

`x=(log(2))/(log(32)) \\x=0.2`

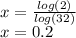
We can also answer this by trying to solve the exponential equation:

`32^x=2`

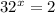
Where we are asked what is the exponent (x) at which we need to raise the base (32) in order to obtain the answer "2"?

Notice that since

`2^5=32`

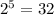
Then
`32^(1/5) = 2`

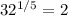
And 1/5 = 0.2 which also agrees with our previous answer