Question

Determine which functions have two real number zeros by calculating the discriminant, b2 – 4ac. Check all that apply.

f(x) = x2 + 6x + 8
g(x) = x2 + 4x + 8
h(x) = x2 – 12x + 32
k(x) = x2 + 4x – 1
p(x) = 5x2 + 5x + 4
t(x) = x2 – 2x – 15

Answer 1

1,3,4,6

Explanation:

EDGE

Answer 2

Explanation:

We need to write the function that have two real number zeros by calculating the discriminant i.e.
`b^2-4ac`.

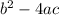We know that,

If D>0 the roots are real and unequal

If D= 0 roots are real and equal

If D< 0 roots are imaginary or not real and unequal

Function (1)

`f(x)=x^2 + 6x + 8\\\\D=6^2-4* 1* 8\\\\D=4`

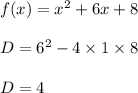
D>0 the roots are real and unequal

Function (2)

`g(x)=x^2 + 4x + 8\\\\D=4^2-4* 1* 8\\\\D=-16`

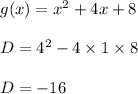
D<0 the roots are real and unequal

Function (3)

`h(x)=x^2 -12x+32\\\\D=(-12)^2-4* 1* 32\\\\D=16`

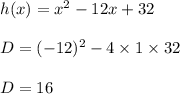
D>0 the roots are real and unequal

Function (4)

`k(x)=x^2 +4x-1\\\\D=(4)^2-4* 1* (-1)\\\\D=20`

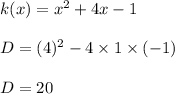
D>0 the roots are real and unequal

Function (5)

`p(x)=5x^2 +5x+4\\\\D=(5)^2-4* 5* 4\\\\D=-55`

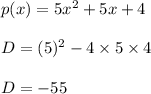
D<0 the roots are real and unequal

Function (6)

`t(x)=x^2 -2x-15\\\\D=(-2)^2-4* 1* (-15)\\\\D=64`

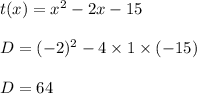
D>0 the roots are real and unequal

(1),(3),(4) and (6) have two real number zeroes.