Answer:
Explanation:
The mean SAT score is
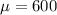 , we are going to call it \mu since it's the "true" mean
, we are going to call it \mu since it's the "true" mean
The standard deviation (we are going to call it
 ) is
) is

Next they draw a random sample of n=70 students, and they got a mean score (denoted by
 ) of
) of
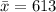
The test then boils down to the question if the score of 613 obtained by the students in the sample is statistically bigger that the "true" mean of 600.
- So the Null Hypothesis
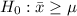
- The alternative would be then the opposite
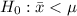
The test statistic for this type of test takes the form
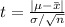
and this test statistic follows a normal distribution. This last part is quite important because it will tell us where to look for the critical value. The problem ask for a 0.05 significance level. Looking at the normal distribution table, the critical value that leaves .05% in the upper tail is 1.645.
With this we can then replace the values in the test statistic and compare it to the critical value of 1.645.
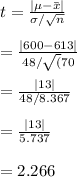
since 2.266>1.645 we can reject the null hypothesis.