Question

A pyramid has a square base and a height of 6 ft. The volume of the pyramid is 162 ft^3. Let s be the length of a side of the pyramid's base.

A) In terms of s, the area of the base is ____________ .
B) The formula for the volume of a pyramid gives the equation ___________.
C) Solving this equation shows that s = __________

Answer 1

`(a)s^2\\(b)162=2s^2\\(c)s=9$ ft`

Explanation:

(a)Base Area

Side length of square base=s

Area of a Square of side length s=
`s^2$ ft^2`

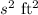
(b)

• Height =6 ft
• Volume=
  `162 $ ft^3.`

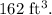
Volume of a Pyramid
`=(1)/(3)X$Base Area X Height`

Substituting the given values, we have:

`162=(1)/(3)Xs^2 X 6\\\\162=2s^2`

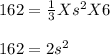
(c)Solving the equation derived from (b)

`162=2s^2\\$Divide both sides by 2\\s^2=81\\s^2=9^2\\s=9$ ft`

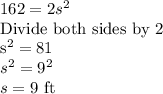
Solving this equation shows that s =9 ft.