Question

In a new experimental teaching method, when students have questions in class, they send them to the instructor via a laptop computer. From time to time, the instructor pauses to read the questions and to provide the answers, without revealing the identities of the students who are asking the questions. This new method is supposed to eliminate the reluctance of students to ask questions for fear of revealing their lack of understanding in public. In a study of this new method, 69 male students and 73 female students participated. Treat these as if they were simple random samples. Of the male students, 38 said that they liked the new method better than the traditional one in which students raise their hands to ask questions. Of the female students, only 20 said they liked the new method better

(a) Construct a 95% confidence interval for the difference between the proportions of male and female students who like the new method better. Let p1, denote the proportion of male students who like the new method better and let p2 denote the proportion of female students who like the new method better.
(b) A 95% confidence interval for the difference between the proportions of male and female students who like the new method better is __________.

Answer 1

a) (0.124, 0.435)

b) I am 95% confident that the proportion difference is between 0.124 and 0.435

Explanation:

Given that:

For male students: number of male students (
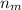`n_m`) = 69, number who liked the new method (x) = 38

For female students: number of female students (
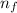`n_f`) = 73, number who liked the new method (x) = 20

a) The probability that a male student like the new method (
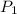`P_1`) is given as:

`P_1=(38)/(69) =0.55`

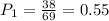
The probability that a female student like the new method (
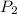`P_2`) is given as:

`P_2=(20)/(73) =0.27`

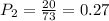
c = 95%, α = 1 -c = 0.05

`z_{(\alpha )/(2) }=1.96`

the difference between the proportions of male and female students who like the new method better =
`P_1-P_2` ±
`z_{(\alpha )/(2) }\sqrt{(P_1(1-P_1))/(n_m) +(P_2(1-P_2))/(n_f)}` =
`0.55-0.27` ±
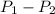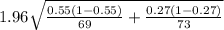`1.96\sqrt{(0.55(1-0.55))/(69) +(0.27(1-0.27))/(73)}` = (0.124, 0.435)

b) I am 95% confident that the proportion difference is between 0.124 and 0.435