Answer:
Organizations can use one-sample hypothesis test to determine if there are performance issues in many ways.
It can be applied to the performance of a sector, a machine, a product, an advertising campaing, etc.
For example, we can take the example of a machine. It may be claimed that a specific machine performs significantly worse than the average.
This average would be the population mean: the average performance of the machines of the same type or process.
Then, a sample of the performance of the machine in study is taken and the hypothesis test can be performed to test the claim that this machine performs significantly worse.
Explanation:
For example, we have an historic performance for this type of machine of 100 units a day. The machine A in study is sampled 14 days and have a performance of 92 units a day, with a sample standard deviation of 12 units/day. We have to test the claim that the machine A makes less units per day than the average.
Then, the null and alternative hypothesis are:
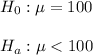
The significance level is 0.05.
The sample has a size n=14.
The sample mean is M=92.
As the standard deviation of the population is not known, we estimate it with the sample standard deviation, that has a value of s=12.
The estimated standard error of the mean is computed using the formula:
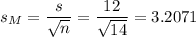
Then, we can calculate the t-statistic as:
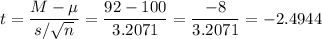
The degrees of freedom for this sample size are:
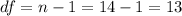
This test is a left-tailed test, with 13 degrees of freedom and t=-2.4944, so the P-value for this test is calculated as (using a t-table):

As the P-value (0.0134) is smaller than the significance level (0.05), the effect is significant.
The null hypothesis is rejected.
There is enough evidence to support the claim that machine A produces significantly less units per day than the average.