Answer:
2.6 m
Explanation:
In the attached diagram
Consider Triangle ABC
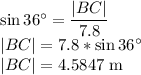
Our goal is to determine the distance of Jen (at point A) to Holly (at Point D).
In Triangle ABC
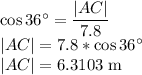
In Triangle BDC
Applying Pythagoras Theorem

Now, |AC|=|AD|+|DC|
6.3103=|AD|+3.7136
|AD|=6.3103-3.7136
|AD|=2.5967
|AD|=2.6m (correct to the nearest tenth of a metre)
The distance of Jen from Holly is 2.6m.