Question

Enrollment in a dance studio has grown exponentially since the studio opened. A graph depicting this growth is shown. Determine the percentage rate of growth.

0.25%
1.25%
2.5%
25%

Answer 1

25%

Explanation:

did test and it was right

Answer 2

Option (4). 25%

Explanation:

The graph attached shows the exponential growth.

Let the graphed function is y =
`(1+(r)/(100))^(t)`

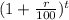
Here 'r' = Rate of growth

t = Duration of time in years

y = enrollments after time 't' years

Graph shows at time 't' = 0 or initially number of enrollments = 20

After 8 years number of enrollments will be

120 =
`20(1+(r)/(100))^(8)`

`(120)/(20)=(1+(r)/(100))^(8)`

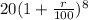
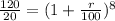
6 =
`(1+(r)/(100))^(8)`

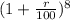
log 6 =
`8\text{log}(1+(r)/(100))`

0.77815 =
`8\text{log}(1+(r)/(100))`

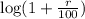`\text{log}(1+(r)/(100))` = 0.0972689

`(1+(r)/(100))=1.251`

`(r)/(100)=0.251`

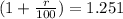
r = 25.1%

r ≈ 25%

Therefore, Option (4) will be the answer.