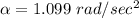Answer:
The final angular velocity is
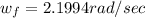
The angular acceleration is
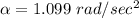
Step-by-step explanation:
From the question we are told that
The radius of each plate is
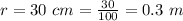
The mass of each plate is
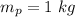
The angular speed of the spinning plate is
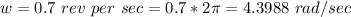
From the law of conservation of momentum

Where
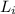 is the initial angular momentum of the system (The spinning and stationary plate ) which is mathematically represented as
is the initial angular momentum of the system (The spinning and stationary plate ) which is mathematically represented as

here
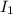 is the moment of inertia of the spinning plate which mathematically represented as
is the moment of inertia of the spinning plate which mathematically represented as
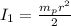
and the zero signify that the stationary plate do not have an angular momentum as it is at rest at the initial state
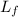 is the final angular momentum of the system (The spinning and stationary plate) , which is mathematically represented as
is the final angular momentum of the system (The spinning and stationary plate) , which is mathematically represented as

Where
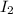 is the moment of inertia of the second plate (This was stationary before but now it spinning due to the first pate ) and is equal to
is the moment of inertia of the second plate (This was stationary before but now it spinning due to the first pate ) and is equal to
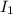
and
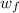 is the final angular speed
is the final angular speed
So we have
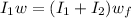
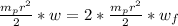
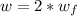
substituting values
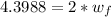
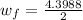
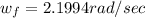
The the rotational impulse-momentum theorem can be mathematially represented as
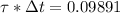
Where
 is the torque and
is the torque and
 is the change in time
is the change in time
So at
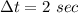
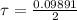

now the angular acceleation is mathematically represented as

substittuting values