Question

Find the QUADRATIc equation 100 POINTS PLS HELP (1,6),(2,19),(3,38),(4,63),(5,94)

Answer 1

`\displaystyle 3 {x}^(2) + 4x - 1 = 0`

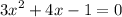
Explanation:

we are given some coordinates

(1,6),(2,19),(3,38),(4,63),(5,94)

we want to figure out the quadratic equation which passes those coordinates

notice that, the coordinates in quadratic sequence

we know that,

A sequence is quadratic if and only if it has second difference

recall that,

• 
  `\displaystyle 2a=2^{ \text{nd }} \text{diff}`
• 
  `\displaystyle 3a + b = U_(2)-U_1`
• 
  `\displaystyle a + b + c = U_1`

these formulas are necessary to figure out a,b and c

because we know that

Quadratic equation standard form:

`\displaystyle a {x}^(2) + bx + c = 0`

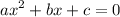
therefore to figure out a,b and c these formulas are important

let's figure out a:

we got that 2nd difference is 6 thus

`\displaystyle 2a = 6`

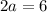
divide both sides by 2

`\displaystyle (2a)/(2) =( 6)/(2)`

`\displaystyle a = 3`

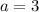
let's figure out b:

by using the second formula we can figure out b

our
`U_1` and
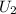`U_2` are 6 and 19 respectively

substitute:

`3 \cdot 3 + b = 19 - 6`

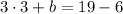
simplify multiplication:

`9+ b = 19 - 6`

simplify substraction:

`9+ b = 13`

cancel 9 from both sides:

`b = 4`

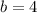
let's figure out c:

our
`U_1` is 6

substitute:

`\displaystyle 3 + 4 + c = 6`

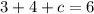
simplify addition:

`\displaystyle 7 + c = 6`

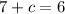
cancel 7 from both sides:

`\displaystyle c = - 1`

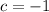
altogether substitute a,b and c to quadratic equation:

`\displaystyle 3 {x}^(2) + 4x - 1 = 0`

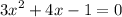
and we are done!