Answer:
Ein: 2.75*10^-3 N/C
Step-by-step explanation:
The induced electric field can be calculated by using the following path integral:

Where:
dl: diferencial of circumference of the ring
circumference of the ring = 2πr = 2π(5.00/2)=15.70cm = 0.157 m
ФB: magnetic flux = AB (A: area of the loop = πr^2 = 1.96*10^-3 m^2)
The electric field is always parallel to the dl vector. Then you have:
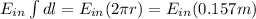
Next, you take into account that the area of the ring is constant and that dB/dt = - 0.220T/s. Thus, you obtain:
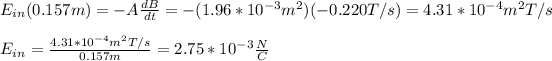
hence, the induced electric field is 2.75*10^-3 N/C