Question

A college entrance exam company determined that a score of 24 on the mathematics portion of the exam suggests that a student is ready for​ college-level mathematics. To achieve this​ goal, the company recommends that students take a core curriculum of math courses in high school. Suppose a random sample of 250 students who completed this core set of courses results in a mean math score of 24.5 on the college entrance exam with a standard deviation of 3.3.

a) Do these results suggest that students who complete the core curriculum are ready for​ college-level mathematics? That​ is, are they scoring above 24 on the math portion of the​ exam?
b) State the appropriate null and alternative hypotheses.

Answer 1

a) The Z -value 2.397 < 2.576 at 99% or 0.01% level of significance

Null hypothesis is accepted at 0.01% level of significance

They score is above 24 on the math portion of the​ exam

b)

Null Hypothesis: There is no significance difference between the college level mathematics and math courses in high school

H₀: μ = 24

Alternative Hypothesis: H₁: μ ≠ 24

Explanation:

Step(i):-

Given random sample 'n' = 250

Given data sample mean x⁻ = 24.5

Standard deviation = 3.3

Null Hypothesis: There is no significance difference between the college level mathematics and math courses in high school

H₀: μ = 24

Alternative Hypothesis: H₁: μ ≠ 24

test statistic

`Z = (x^(-) - mean)/((S.D)/(√(n) ) )`

`Z = (24.5 - 24)/((3.3)/(√(250) ) ) = (0.5)/(0.2087) = 2.397`

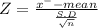
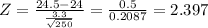
a) 99% or 0.01% level of significance

Level of significance ∝ = 0.01

`Z_{(\alpha )/(2) } = Z_{(0.01)/(2) } = Z_(0.005) =2.576`

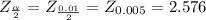
The Z -value 2.397 < 2.576 at 99% or 0.01% level of significance

Null hypothesis is accepted at 0.01% level of significance

They score is above 24 on the math portion of the​ exam

b) 95% or 0.05% level of significance

Level of significance ∝ = 0.05

`Z_{(\alpha )/(2) } = Z_{(0.05)/(2) } = Z_(0.025) = 1.96`

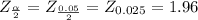
The Z -value 2.397 > 1.96 at 95% or 0.05% level of significance

Null hypothesis is Rejected at 0.05% level of significance

They score is below 24 on the math portion of the​ exam