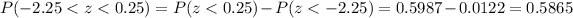Answer:
i and iii) In the figure attached part a we have the illustration for the area required for the probability of less than 2 hours and in b the illustration for the probability that X would be between 2 and 4
ii)
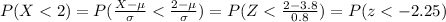
And using the normal standard table or excel we got:
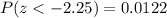
iv)
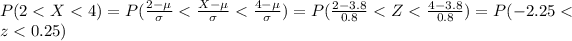
And we can find the probability with the following difference and usint the normal standard distirbution or excel and we got:
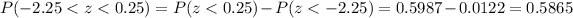
Explanation:
Let X the random variable that represent amount of time people spend exercising in a given week, and for this case we know the distribution for X is given by:
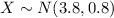
Where
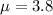 and
and
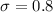
Part i and iii
In the figure attached part a we have the illustration for the area required for the probability of less than 2 hours and in b the illustration for the probability that X would be between 2 and 4
Part ii
We are interested on this probability:
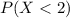
We can use the z score formula given by:

Using this formula we have:
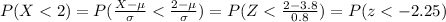
And using the normal standard table or excel we got:
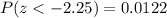
Part iv
We want this probability:
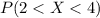
Using the z score formula we got:
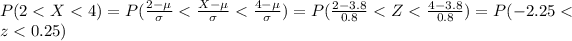
And we can find the probability with the following difference and usint the normal standard distirbution or excel and we got: