Question

A bond analyst is analyzing the interest rates for equivalent municipal bonds issued by two different states.

a) At α = 0.05, is there enough evidence to conclude that there is a difference in the interest rates paid by the two states?
State A:
Sample size 60
Mean interest rate (%) 3.2
Population variance .02
State B:
Sample size 60
Mean interest rate (%) 3.4
Population variance .05

Answer 1

`z=\frac{(3.2-3.4)-0}{\sqrt{(0.141^2)/(60)+(0.224^2)/(60)}}}=-5.85`

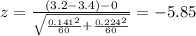
The p value can be calculated with this probability:

`p_v =2*P(z<-5.85)=4.91x10^(-9)`

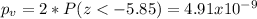
The p value for this case is a value very low and near to 0 so then we have enough evidence to reject the null hypothesis and we can conclude that the true means for this case are significantly different

Explanation:

Information provided

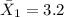`\bar X_(1)=3.2` represent the mean for sample A

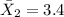`\bar X_(2)=3.4` represent the mean for sample B

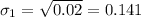`\sigma_(1)=√(0.02)= 0.141` represent the sample standard deviation for A

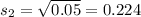`s_(2)=√(0.05)= 0.224` represent the sample standard deviation for B

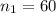`n_(1)=60` sample size for the group A

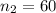`n_(2)=60` sample size for the group B

`\alpha=0.05` Significance level provided

z would represent the statistic

Hypothesis to test

We want to verify if that there is a difference in the interest rates paid by the two states, the system of hypothesis would be:

Null hypothesis:
`\mu_(1)-\mu_(2)=0`

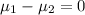
Alternative hypothesis:
`\mu_(1) - \mu_(2)\\eq 0`

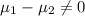
The statistic for this case since we know the population deviations is given by:

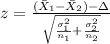`z=\frac{(\bar X_(1)-\bar X_(2))-\Delta}{\sqrt{(\sigma^2_(1))/(n_(1))+(\sigma^2_(2))/(n_(2))}}` (1)

Replacing the info given we got:

`z=\frac{(3.2-3.4)-0}{\sqrt{(0.141^2)/(60)+(0.224^2)/(60)}}}=-5.85`

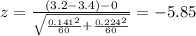
The p value can be calculated with this probability:

`p_v =2*P(z<-5.85)=4.91x10^(-9)`

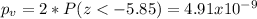
The p value for this case is a value very low and near to 0 so then we have enough evidence to reject the null hypothesis and we can conclude that the true means for this case are significantly different