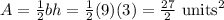Answer:
Using Geometry to answer the question would be the simplest:
Explanation:
Remembering the formula for the area of a triangle which is
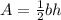 . One can then tackle the question by doing the following:
. One can then tackle the question by doing the following:
Step 1 Find the y-intercepts
The y-intercepts are found by substituting in
 .
.
Which gives you this when you plug it into both equations:
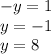
So the y-intercepts for the graphs are
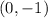 , and
, and
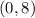 respectively.
respectively.
Now one has to use elimination to solve the problems by adding up the equations we get:
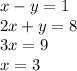
Now to solve for the y component substitute:
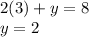
Therefore, the graphs intersect at the following:
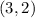
Now we have our triangle which is accompanied by the graph.
now to solve it we must figure out how long the base is:
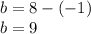
The height must also be accounted for which is the following:
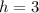
Now the formula can be used: