Question

During an experiment of momentum, trolley, X, of mass (2.34 ± 0.01) kg is moving away from another trolley, Y, of mass (2.561 ± 0.001) kg with a speed of (3.2 ± 0.01) ms-1. The second trolley is moving away with a distance of (2.5 ± 0.01) ms-1.

What is the absolute uncertainty of the ratio of momentum of the two trolleys X/Y?

Answer 1

P = 1 (14,045 ± 0.03 ) k gm/s

Step-by-step explanation:

In this exercise we are asked about the uncertainty of the momentum of the two carriages

Δ (Pₓ / Py) =?

Let's start by finding the momentum of each vehicle

car X

Pₓ = m vₓ

Pₓ = 2.34 2.5

Pₓ = 5.85 kg m

car Y

Py = 2,561 3.2

Py = 8,195 kgm

How do we calculate the absolute uncertainty at the two moments?

ΔPₓ = m Δv + v Δm

ΔPₓ = 2.34 0.01 + 2.561 0.01

ΔPₓ = 0.05 kg m

Δ
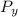`P_(y)` = m Δv + v Δm

ΔP_{y} = 2,561 0.01+ 3.2 0.001

ΔP_{y} = 0.03 kg m

now we have the uncertainty of each moment

P = Pₓ /
`P_(y)`

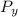
ΔP = ΔPₓ/P_{y} + Pₓ ΔP_{y} / P_{y}²

ΔP = 8,195 0.05 + 5.85 0.03 / 8,195²

ΔP = 0.006 + 0.0026

ΔP = 0.009 kg m

The result is

P = 14,045 ± 0.039 = (14,045 ± 0.03 ) k gm/s