Answer:
For this case we can define y as the response variable and represent the cost and x the independent variable who represent the hours of lessons. We know that the instructor has an initial fee of 12 and charges 8 per hour. So then we can model the situation with this formula:
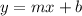
Where m = 8 represent the slope and b =12 the intercept so our model would be:
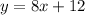
And the y intercept would be at x=0 and y=12 and represent the initial amount of money that we need to pay in order to have the instructor.
Step-by-step explanation:
For this case we can define y as the response variable and represent the cost and x the independent variable who represent the hours of lessons. We know that the instructor has an initial fee of 12 and charges 8 per hour. So then we can model the situation with this formula:
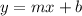
Where m = 8 represent the slope and b =12 the intercept so our model would be:
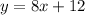
And the y intercept would be at x=0 and y=12 and represent the initial amount of money that we need to pay in order to have the instructor.