Answer:
0.0228
Explanation:
Let us assume that the mean (μ) = 2 and the standard deviation (σ) = 0.5
Z score is a standard score used to measure the number of standard deviations by which the raw score (x) is above or below the mean. It is given by the equation:

For x > 3
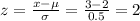
From the normal distribution table, P(x > 3) = P(z > 2) = 1 - P(z < 2) = 1 - 0.9772 = 0.0228