Question

use pascal’s triangle or the binomial theorem to find the coefficient on the m3 term in the expression of (2m-1)^4

Answer 1

`= 16m^(4)-32m^(3)+24m^(2)-8m+1`

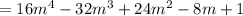
Explanation:

According to pascal triangle, in order to expand the expression
`(a+b)^(n)`, the power of a will be reducing by 1 while the power of b will be increasing by until we reach the highest power n. after the expansion, then we fix the coefficients according to pascal triangle. The coefficient of the expansion varies depending on the power of the expansion.

For power of 0. the coefficient is 1

For power of 1. the coefficient is 1, 1

For power of 2. the coefficient is 1, 2, 1

For power of 3. the coefficient is 1, 3, 3, 1

For power of 4. the coefficient is 1,4, 6, 4, 1 and so on

`(a+b)^(n)\\a^(n)b^(n) + a^(n-1)b^(n+1) +a^(n-2)b^(n+2) +...`

`Given\ (2m-1)^(4)\\on\ expansion;\\= (2m)^(4)(-1)^(0) + (2m)^(3)(-1)^(1) +(2m)^(2)(-1)^(2) + (2m)^(1)(-1)^(3) + (2m)^(0)(-1)^(4)\\= 16m^(4)+8m^(3)(-1)+4m^(2) (1)+2m(-1)+1\\= 16m^(4)-8m^(3)+4m^(2)-2m+1\\\\`

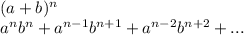
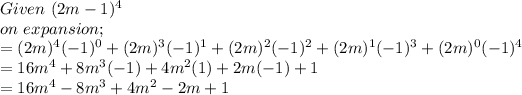
Fixing the coefficient since the power is 4, we will use the coefficient 1,4,6,4,1 according to pascals to have;

`= (1)16m^(4)-(4)8m^(3)+(6)4m^(2)-(4)2m+(1)1\\= 16m^(4)-32m^(3)+24m^(2)-8m+1`

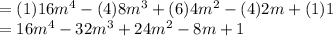
This gives the required expansion