Question

A level differentiation question. Mainly stuck on the 4-x/x part. Help would be appreciated.

Answer 1

see explanation

Explanation:

Differentiate
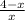`(4-x)/(x)` using the quotient rule, given

y =
`(f(x))/(g(x))` , then

`(dy)/(dx)` =
`(g(x)f'(x)-f(x)g'(x))/(g(x)^2)`

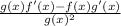
Here f(x) = 4 - x ⇒ f'(x) = - 1

g(x) = x ⇒ g'(x) = 1 , thus

`(dy)/(dx)` =
`(-x-(4-x))/(x^2)` =
`(-x-4+x)/(x^2)` = -
`(4)/(x^2)`

-----------------------------------------

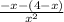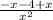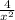
Given

y = 3x² +
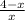`(4-x)/(x)`, then

`(dy)/(dx)` = 6x -
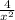`(4)/(x^2)` ← evaluate for x = 2

`(dy)/(dx)` = 6(2) -
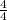`(4)/(4)` = 12 - 1 = 11 ← as required

Let me know if you require assistance on (b) and (c)