Question

A car of 900 kg mass is moving at the velocity of 60 km/hr. It is brought into rest at 50 meter distance by applying a brake. Now, calculate the force required to stop the car.

Answer 1

Answer:
`-2502N`

Step-by-step explanation:

`(V_2)^2=(V_1)^2+2ad`

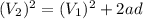
where;

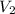`V_2` = final velocity = 0

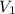`V_1` = initial velocity = 60 km/h = 16.67 m/s

`a` = acceleration

`d` = distance

First all of, because acceleration is given in m/s and not km/h, you need to convert 60km/h to m/s. Our conversion factors here are 1km = 1000m and 1h = 3600s

`60km/h((1000m)/(1km) )((1h)/(3600s) )=16.67m/s`

Solve for a;

`(V_2)^2=(V_1)^2+2ad`

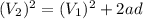
Begin by subtracting
`(V_1)^2`

`(V_2)^2-(V_1)^2=2ad`

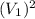
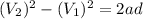
Divide by 2d

`((V_2)^2-(V_1)^2)/(2d) =a`

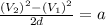
Now plug in your values:

`a=((0)^2-(16.67 m/s)^2)/(2(50m))`

`a=(0-277.89m^2/s^2)/(100m)`

`a=-2.78m/s`

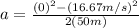
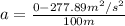
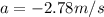
If you're wondering why I calculated acceleration first is because in order to find force, we need 2 things: mass and acceleration.

`F=ma`

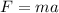
m = mass = 900kg

a = acceleration = -2.78m/s

`F=(900kg)(-2.78m/s)\\F=-2502N`

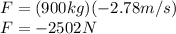
It's negative because the force has to be applied in the opposite direction that the car is moving.