Question

During an experiment of momentum, trolley, X, of mass (2.34 ± 0.01) kg is moving away

from another trolley, Y, of mass (2.561 ± 0.001) kg with a speed of (3.2 ± 0.01) ms
-1
. The
second trolley is moving away with a distance of (2.5 ± 0.01) ms-1
.
What is the absolute uncertainty of the ratio of momentum of the two trolleys
X
Y
?
Please I really need the answer of this question. Can somebody here do it for me?

Answer 1

Answer: The ratio X/Y is (1.172 ± 97.667)

Explanation: Absolute uncertainty is the value that when combined with a reported number, gives the range of the number.

Momentum is a quantity of motion an object has. It is calculated as a relation between mass of an object and its velocity: p = m.v

For the trolley X, momentum is:

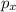`p_(x)` = (2.34 ± 0.01)*(3.2 ± 0.01)

and for trolley Y, momentum is:

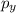`p_(y)` = (2.561 ± 0.001)*(2.5 ± 0.01)

To solve the multiplications:

For x:

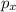`p_(x)` = 2.34*3.2 = 7.5

relative uncertainty =
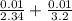`(0.01)/(2.34) + (0.01)/(3.2)` = 0.0074

absolute uncertainty = 7.5*0.0074 = 0.055

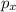`p_(x)` = 7.5 ± 0.055

For y:

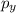`p_(y)` = 2.561*2.5 = 6.4

relative uncertainty =
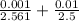`(0.001)/(2.561) + (0.01)/(2.5)` = 0.0044

absolute uncertainty = 6.4*0.0044 = 0.028

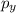`p_(y)` = 6.4 ± 0.028

The ratio of momentum:

`(p_x)/(p_y)` = (7.5 ± 0.055) ÷ (6.4 ± 0.028)

Dividing absolute uncertainty, the rules are the same for multiplication.

`(p_x)/(p_y)` =
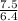`(7.5)/(6.4)` = 1.172

relative uncertainty =
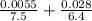`(0.0055)/(7.5) + (0.028)/(6.4)` = 0.012

absolute uncertainty = 1.172*0.012 = 97.667

`(p_x)/(p_y)` = 1.172 ± 97.667

The ratio of momentum of the 2 trolleys is 1.172 ± 97.667.