Question

What is the diameter of a hemisphere with a volume of 73802 ft^3 to the nearest tenth of a foot?

Answer 1

65.6

Explanation:

Answer 2

375.4 ft

Explanation:

Volume of sphere is given by
`(4\pi r^3)/3`

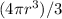
where is the radius

since hemisphere is half of sphere, its volume is half of volume of sphere

Volume of hemisphere is given by
`(1/2)(4\pi r^3)/3 = (2\pi r^3)/3`

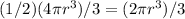
Given volume of sphere is 73802 ft^3.

equating this value with formula for Volume of hemisphere, we have

`(2\pi r^3)/3 = 73802 ft^3 \\=>\pi r^3 = 3/2( 73802) ft^3\\=>22/7 r^3 = 110,703 ft^3\\=> r^3 = 7/22(110,703 )ft^3\\=> r^3 = 35223.6818\\=> r = √(35223.6818)\\=> r = 187.679`

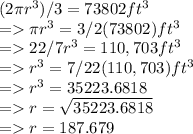
Thus, radius of hemisphere is 187.679 ft

we know that diameter is twice of radius

therefore

diameter of hemisphere = 2*187.679 ft = 375.358 ft.

diameter of hemisphere to the nearest tenth of a foot= 375.4 ft