Answer:
Height of the mountain was 28331.8 feet.
Explanation:
An observer took the measurements from two sights C and D.
Point D was 1000 ft away from the earlier sight point C.
Angle of elevations from points C and D were 85° and 83° respectively.
From ΔABC,
tan85 =
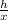
x =
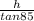 -----(1)
-----(1)
Similarly, from ΔABD,
tan83 =

x + 1000 =
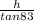
x =
 -----(2)
-----(2)
Now we substitute the value of x from equation (1) in the equation (2)
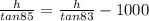
0.122785h - 0.087488h = 1000
0.035296h = 1000
h = 28331.822 ft
h ≈ 28331.8 ft
Therefore, height of the mountain was 28331.8 feet.