Question

Arial says that, for any pair of linear relations, if the coefficients of the y-terms are equal and the coefficients of the x-terms are equal, the graphs of the two lines will be parallel.

a. Give an example for which Arial's claim is true.

b. Give an example for which Arial's claim is false.

c. Suggest an improvement to Arial's claim.

Answer 1

a. Give an example for which Arial's claim is true.

If linear relations have equal coefficient about the independent variable, then those linear relations are parallel. For example,
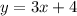`y=3x+4` and
`y=3x-5`.

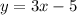Notice that the coefficient of the dependent variable must be also equal, otherwise it would change the slope of the expression and they wouldn't be parallel.

b. Give an example for which Arial's claim is false.

The statement is not false.

c. Suggest an improvement to Arial's claim.

An improvemente would be that the constant term no need to be equal too, between linear relations, because they can be at "differecent heights", sort of speak.