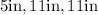Question

The dimensions of a chocolate box are: height=x + 2 inches, length=2x+5 inches, and width=4x-1 inches. If the volume of the chocolate box is 605 cubic inches, what is the value of x?

Answer 1

To begin to answer your question you would need to know that the formula for the volume of a rectangular prism is the following:
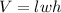`V=lwh`. Now its just a manner of substitutions.

Explanation:

`V=605 \text{in}^3`

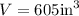
Then one can also state the following:

`V=(x+2)(4x-1)(2x+5)`

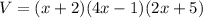
Following up with this substitution:

`605=(x+2)(4x-1)(2x+5)`

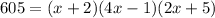
Proceeding with a FOIL procedure:

`605=(4x^2+8x-x-2)(2x+5)`

`605=8x^(3)+34x^(2)+31x-10`

`0=8x^(3)+34x^(2)+31x-615`

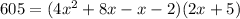
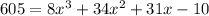
Using PRZs:

`PRZs=\frac{\text{Factors of Constant Term}}{\text{Factors of Highest Power}}=(\pm 1,\pm 3, \pm 5, \pm 41, \pm 615)/(\pm 1, \pm 2, \pm 4, \pm 8)`

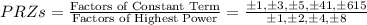
By graphing it one can identify that 3 is a solution so plugging it in and using synthetic division.

`\begin{array}{ccccc}3|& 8 & 34 & 31 & -615\\ \ \ |& & 24 & 174 & 615 \\ & 8 & 58 & 205 &0 \end{array}\\`

Giving the following the polynomial:

`0=(x-3)(8x^2+58x+205)`

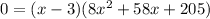
Now one can evaluate the discriminant of that quadratic:

`58^2-4(8)(205)=-3196`

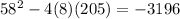
Because it is negative one knows that it produces imaginary solutions. Therefore the only real solution is
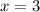`x=3`. Therefore the dimension of the box is the following:
`5\text{in},11\text{in}, 11\text{in}`

Answer 2

I hope this helps you