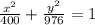Answer:
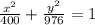
Explanation:
The distance between foci with respect to origin is determined by mean of the Pythagorean Theorem:
![2\cdot c = \sqrt{(0-0)^(2)+[24-(-24)]^(2)}](https://img.qammunity.org/2021/formulas/mathematics/high-school/siajpu3h69l99najio0d6si2uffyq3vztc.png)
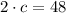

The distance between origin and any of the horizontal co-vertices is:
![a = \sqrt{[10-(-10)]^(2)+(0-0)^(2)}](https://img.qammunity.org/2021/formulas/mathematics/high-school/diwiemovkdgcmxxi7nd32kiko72ojxgpdr.png)

Now, the distance between origin and any of the vertical co-vertices is determined by the following Pythagorean relationship:
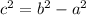
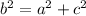
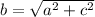
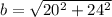

Lastly, the equation of the ellipse in standard form is: