Answer:
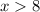
And the other inequality is:
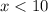
If we use the two conditions we have :
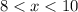
If we use only integers the only possible solution is x =9 and if x is a real number the solution can be infinite numbers between 8 and 9
Explanation:
For this case we define the number of interest as x and we have:
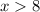
And the other inequality is:
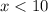
If we use the two conditions we have :
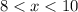
If we use only integers the only possible solution is x =9 and if x is a real number the solution can be infinite numbers between 8 and 9