Answer:
Statements Reasons
1.
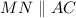 1. Given
1. Given
2.
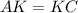 2. Given
2. Given
3.
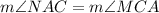 3. Base angles theorem.
3. Base angles theorem.
4.
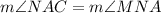 4. Alternate interior angles.
4. Alternate interior angles.
5.
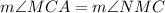 5. Alternate interior angles.
5. Alternate interior angles.
6.
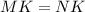 6. Isosceles triangle theorem.
6. Isosceles triangle theorem.
7.
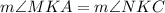 7. Vertical angles.
7. Vertical angles.
8.
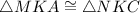 8. By SAS postulate.
8. By SAS postulate.
9.
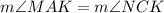 9. By CPCTC.
9. By CPCTC.
10. 10. Sum of adjacent angles.

11.
 is isosceles 11. Base angles theorem.
is isosceles 11. Base angles theorem.