Answer:
none of the above (talk to your teacher about this)
Explanation:
If a polynomial has real coefficients, complex roots come in conjugate pairs.
A root of
 will have a conjugate of
will have a conjugate of
 , which will also be a root.
, which will also be a root.
__
Here, it looks like the given root is
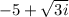 , which is different from
, which is different from
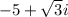 . None of the listed choices is the complex conjugate of this value.
. None of the listed choices is the complex conjugate of this value.
The value of
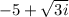 is ...
is ...

so its conjugate is ...
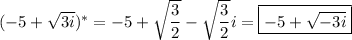
You will note that this is not among the answer choices.
_____
Additional comment
When a problem like this has an error in its presentation, we highly recommend you discuss it with your teacher (to get it corrected or deleted for future students). If you feel you must select one of the (erroneous) answer choices, your computer will probably accept the choice of
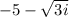 , the first one.
, the first one.