Question

Una barra de longitud de 2 m está cargada uniformemente y tiene una carga total de 5nC. Busqué su potencial eléctrico (relativo acero en el infinito) en un punto que se encuentra a lo largo del eje de la barra y está a 3m del centro de la barra?

Answer 1

11.44J/C

Step-by-step explanation:

To find the electric potential for a point at 3m from one extreme of the bar you use the formula for the electric potential:

`V=\int k(dq)/(r)=\int k(dq)/(x+3)`

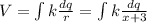
Where r = x+3 represent the 3m distance of the charge to a point x in the bar.

dq: differential of charge = λdx. λ is the linear charge density.

k: Coulomb constant = 8.98*10^9 Nm^2/C^2

You can write dq as λdx. Furthermore, If you assume that the other extreme of the bar is at origin of the x-axis you can write the integral as follow:

`V=\int_(0)^(2)k(\lambda dx)/(x+3)\\\\V=k\lambda \ ln(x+3)|_(0)^(2)=k\lambda (0.510)`

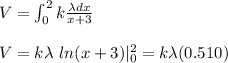
You replace λ ad k in the last expression:

`V=(8.98*10^9Nm^2/C^2)((5*10^(-9)C)/(2m))(0.510)=11.44(J)/(C)`

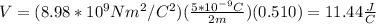
hence, the electric potential is 11.44J/C