Question

Temperature (x) 65 70 75 80 85 90 95 100 105

Number of ice cream cones sold per hour (y) 8 10 11 13 12 16 19 22 23
Note: Critical Value for n = 9 is 0.666

Calculate the linear correlation coefficient r, for temperature (x) and the number of ice cream cones sold per hour (y). (round to 3 decimal place)
Is there a linear relation between the two variables x, and y? Why? If yes, indicate if the relationship is positive or negative. (Hint: Compare the absolute value of r and critical value)
Construct the least-squares regression line for temperature (x) and the number of ice cream cones sold per hour (y) and interpret its slope. (round to 3 decimal place)
Predict the number of ice cream cones sold per hour when the temperature is 80 and calculate the residual for x = 80º. (round to nearest whole number)
Would it be reasonable to use the least-squares regression line to predict the number of ice cream cones sold when it is 50 degrees? Explain your answer.

Answer 1

Explanation:

Hello!

You have to calculate the linear correlation coefficient (r) between the variables

X₁: temperature

X₂: Number of ice cream cones sold per hour.

The formula to calculate the coefficient of linear correlation between the two variables is the following:

`r= \frac{sumX_1X_2-((sumX_1)(sumX_2))/(n) }{\sqrt{[sumX_1^2-((sumX_1)^2)/(n) ][sumX_2^2((sumX_2)^2)/(n) ]} }`

∑X₁= 765; ∑X₁²= 66525 ∑X₂= 134 ∑X₂²= 2228 ∑X₁X₂= 11965 n=9

`r= \frac{11965-(765*134)/(9) }{\sqrt{[66525-((765)^2)/(9) ][2228-((134)^2)/(9) ]} }`

r= 0.97

To test if there is a positive linear association between both variables the statistical hypotheses are:

H₀: ρ ≤ 0

H₁: ρ > 0

critical value 0.666

r= 0.97

The decision is to reject the null hypothesis, there is a positive linear correlation between the temperature and the number of ice cream cones sold per hour.

The regression line is

^Y= a + bX

where

a: represents the estimation of the y-intercept

b: represents the estimation of the slope

`b= (sumXY-(sumXsumY)/(n) )/(sumX^2-((sumX)^2)/(n) )`

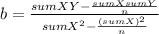
b= 0.38

a= Y[bar]-bX[bar]

a= -17.69

The estimated regression line for the number of ice cream cones and the temperature is ^Y= -17.69 + 0.38Xi

To estimate the number of ice cream cones sold when the temperature is 80º you have to replace the value of X in the estimated regression line:

^Y= -17.69 + 0.38*80= 12.71

It is expected that they will sell 12.71 ≅ 13 ice cream cones when the temperature is 80º

You can use the estimation of the regression line to predict values within the range of definition of the independent variable, in this case from 65º to 105º of temperature, because it is within those values that you can be sure they have a linear association. Below or above you are not certain that their association is linear, it may be, for example exponential, or there may be no association between them.

Example: If the temperature is comfortable or cold, it is more likely that people won't buy ice creams, so for those values it will be no linear association between them.

I hope this helps!