Question

The table shows the estimated number of bees, y, in a hive x days after a pesticide is released near the hive.

A 2-column table with 6 rows. The first column is labeled number of days with entries 0, 10, 20, 30, 40, 50. The second column is labeled estimated number of bees with entries 10,000; 7,500; 5,600; 4,200; 3,200; 2,400.
Which function best models the data?

y = 9,958(0.972)x
y = 0.972(9,958)x
y = 9,219x– 150
y = –150x + 9,219

Answer 1

A. y = 9,958(0.972)x

Explanation:

Answer 2

A.

Explanation:

The given table is

Days Bees

0 10,000

10 7,500

20 5,600

30 4,200

40 3,200

50 2,400

Where
`x` represents days and
`y` represents bees.

The exponential function that models this problem must be like

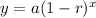`y=a(1-r)^(x)`, which represenst an exponential decary, because in this case, the number of bees decays.

We nned to use one points, to find the rate of decay. We know that
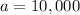`a=10,000`, because it starts with 10,000 bees.

Let's use the points (10, 7500)

`y=a(1-r)^(x)\\7500=10000(1-r)^(10)`

Solving for
`r`, we have

`(7500)/(10000)=(1-r)^(10) \\(1-r)^(10) =0.75`

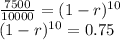
Using logarithms, we have

`ln((1-r)^(10)) =ln(0.75)\\10 * ln(1-r)=ln(0.75)\\ln(1-r)=(ln(0.75))/(10) \approx -0.03\\e^(ln(1-r))=e^(-0.03)\\1-r =e^(-0.03)\\r=-e^(-0.03)+1 \approx 1.97`

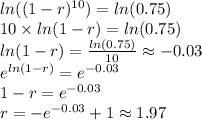
Replacing all values in the model, we have

`y=10000(1-1.97)^(x)\\y=10000(0.97)^(x)`

Therefore, the right answer is the first choice, that's the best approximation to this situation.