Question

Two parallel plates are a distance apart with a potential difference between them. A point charge moves from the negatively charged plate to the positively charged plate. The charge gains kinetic energy 800J. The distance between the plates is tripled and the potential difference between them is halved. What is the kinetic energy gained (in joules) by an identical charge moving between these plates

Answer 1

K' = 1200 J

Step-by-step explanation:

To find the kinetic energy you first take into account the formula for the kinetic energy of the charge:

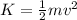`K=(1)/(2)mv^2` = 800J (1)

m: mass of the charge

v: final speed of the charge when it reaches the positively charged plate.

Furthermore, you have that the acceleration of the charge is obtained by using the second Newton law:

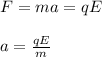`F=ma=qE\\\\a=(qE)/(m)` (2)

a: acceleration

E: electric field

q: charge

The electric field between two parallel plates is V/d, being V the potential difference and d the separation between plates. You replace E in (2) and obtain:

`a=(qV)/(md)`

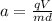
Next, you take into account the following formula for the calculation of the final speed of the charge:

`v^2=v_o^2+2ad\\\\v_o=0m/s\\\\v=\sqrt{(2qVd)/(md)}=\sqrt{(2qV)/(m)}`

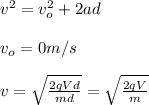
Next, you replace this value of v in (1):

`K=(1)/(2)mv^2=(1)/(2)m((2qV)/(m))=qV` = 880J (3)

If the distance between plates is tripled, and the potential difference is halved, you have for the new final speed:

`v'^2=v'_o^2+2a(3d)\\\\v_o=0m/s\\\\v'=√(6ad)=\sqrt{6((q)/(md))(V)/(2)d}=\sqrt{(3qV)/(m)}`

And the kinetic energy becomes:

`K'=(1)/(2)mv^2=(1)/(2)m((3qV)/(m))=(3)/(2)qV` (4)

You calculate the ratio between both kinetic energies K and K', that is, you divide equations (3) and (4), in order to find the new kinetic energy:

`K=qV=800J\\\\K'=(3)/(2)qV\\\\(K)/(K')=(qV)/(3/2\ qV)=(2)/(3)\\\\K'=(3)/(2)K=(3)/(2)(800J)=1200J`

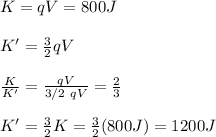
hence, the kinetic energy of the charge incresases to 1200J