Question

How old is a skeleton that has lost 27% of its carbon-14? Use the exponential decay model for carbon-14, A=A0e^-0.000121t Round the answer to the nearest whole number

Answer 1

2,601 years

Explanation:

Given the decay model for carbon-14

`A=A_0e^(-0.000121t)`

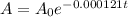
We want to determine the age of a skeleton that has lost 27% of its C-14.

Initial Value of C-14=100%=1

Present Amount, A(t)=100%-27%=73%=0.73

Substituting these into the model, we have:

`0.73=1e^(-0.000121t)\\$Take the natural logarithm of both sides\\ln(0.73)=-0.000121t\\Divide both sides by -0.000121\\t=ln (0.73) / (-0.000121)\\t=2600.9 \approx 2601$ years (to the nearest whole number)`

The skeleton is approximately 2,601 years old.