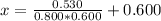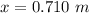Question

What must x be so that the handle end of the bat remains at rest as the bat begins to move? (Hint: Consider the motion of the center of mass and the rotation about the center of mass. Find x so that these two motions combine to give v=0 for the end of the bat just after the collision. Also, note that integration of equation ∑τ⃗ =dL⃗ dt gives ΔL=∫t1t2(∑τ)dt. )

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

Step-by-step explanation:

From the question we are told that

The mass of the bat is
`m_b = 0.800 \ kg`

The bat length is
`L_b = 0.900 \ m`

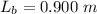
The distance of the bat's center of mass to the handle end is
`z_c = 0.600 \ m`

The moment of inertia of the bat is
`I = 0.0530 \ kg \cdot m^2`

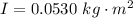
The objective of the solution is to find x which is the distance from the handle of the bat to the point where the baseball hit the bat

Generally the velocity change at the end of the bat is mathematically represented as

`\Delta v_e = \Delta v_c - \Delta w* z_c`

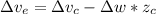
Where
`\Delta v_c` is the velocity change at the center of the bat which is mathematically represented as

`\Delta v_c = (Impulse)/(m_b )`

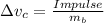
We are told that the impulse is J so

`\Delta v_c = (J)/(m_b )`

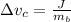
And
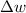`\Delta w` is the change in angular velocity which is mathematically represented as

`\Delta w = (J (z -z_c))/(I)`

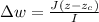
Now we have that

`\Delta v_e = (J)/(m_b ) - [(J (x- z_c))/(I) ] * z_c`

Before a swing when the bat is at rest the velocity change a the end of the bat handle is zero and the impulse will be 1

So

`0 = (1)/(m_b ) - [(J (x- z_c))/(I) ] * z_c`

=>
`x = (I)/(m_b z_c) + m_b`

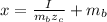
substituting values

`x = (0.530)/(0.800 * 0.600) + 0.600`

`x = 0.710 \ m`