Answer:
Step-by-step explanation:
The question in english is:
A ray of light falls under an angle of incidence of 30 degrees on a flat surface that separates two transparent materials with indexes of refractions 1.60 and 1.40, respectively.
Calculate the angle of refraction (from the environment with the lower index of refraction)
Solution
According to Snell's Law :
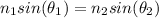
Where:
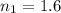 is the first medium index of refraction
is the first medium index of refraction
 is the second medium index of refraction
is the second medium index of refraction
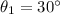 is the angle of the incident ray
is the angle of the incident ray
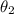 is the angle of the refracted ray
is the angle of the refracted ray
We need to find
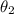 from the equation above,
from the equation above,
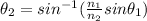
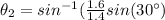
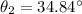
Therefore, the angle of refraction is 34.84°