Answer:
L= 276.4 mm
Step-by-step explanation:
Given that
E= 180 GPa
d= 3.7 mm
F= 1890 N
ΔL= 0.45 mm
We know that ,elongation due to load F in a cylindrical bar is given as follows


Now by putting the values in the above equation we get
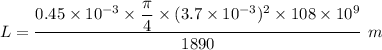
L=0.2764 m
L= 276.4 mm
Therefore the length of the specimen will be 276.4 mm