Question

The motion of a set of particles moving along the x-axis is governed by the differential equation dx dt = t 3 - x3, where x1t2 denotes the position at time t of the particle. (a) If a particle is located at x = 1 when t = 2, what is its velocity at this time? (b) Show that the acceleration of a particle is

Answer 1

a)V=7 m/s

b)a=3t²-3x² t³ +3 x ⁵

Step-by-step explanation:

Given that

`(dx)/(dt)=t^3-x^3`

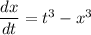
a)

We know that velocity V is given as follows

`V=(dx)/(dt)`

`V=t^3-x^3`

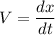
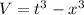
At t= 2 s and x= 1 m

`V=2^3-1^3=7 m/s`

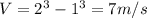
V=7 m/s

b)

Acceleration a is given as follows

`a=(dV)/(dt)`

`a=3t^2-3x^2(dx)/(dt)`

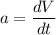
Now by putting the values

`a=3t^2-3x^2* (t^3-x^3)`

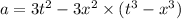
a=3t²-3x² t³ +3 x ⁵

Therefore the acceleration of a particle will be 3t²-3x² t³ +3 x ⁵.