Answer:
(a) 95% of people has an IQ score between 66 and 134.
(b) 5% of people has an IQ score less than 66 or greater than 134.
(c) 2.5% of people has an IQ score greater than 134.
Explanation:
We are given that Scores of an IQ test have a bell-shaped distribution with a mean of 100 and a standard deviation of 17.
Let X = Scores of an IQ test
So, X ~ Normal(
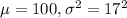 )
)
Now, the Empirical rule states that;
- 68% of the data values lies within one standard deviation of the means.
- 95% of the data values lies within two standard deviation of the means.
- 99.7% of the data values lies within three standard deviation of the means.
That is; [
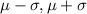 ] = [
] = [
 ]
]
=
![[83,117]](https://img.qammunity.org/2021/formulas/mathematics/college/phhu9wf6mo6ognzxz780yexgot2i4183wj.png)
[
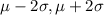 ] = [
] = [
 ]
]
=
![[66,134]](https://img.qammunity.org/2021/formulas/mathematics/college/vd74r3xtkk6w8h8bd7fssm8yh8spn298zp.png)
[
 ] = [
] = [
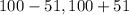 ]
]
=
![[49,151]](https://img.qammunity.org/2021/formulas/mathematics/college/5v8r5xq0sgg8po67i8ejf00ckz2beoj3ef.png)
(a) Percentage of people that has an IQ score between 66 and 134 is given by = P(66 < X < 134)
As seen above this value lies in the second category which means that 95% of people that has an IQ score between 66 and 134.
(b) Percentage of people that has an IQ score less than 66 or greater than 134 is given by;
As we know that 95% of the data values lies within 66 and 134, so the percentage of people that has an IQ score less than 66 or greater than 134 is = 100% - 95% = 5%.
(c) Since it has been calculated above that 5% of people has an IQ score less than 66 or greater than 134 which means half of these people will lie below score of 66 and half of these will lie above score of 134.
SO, percentage of people that has an IQ score greater than 134 =
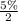 = 2.5%
= 2.5%
Hence, 2.5% of people has an IQ score greater than 134.