Question

Firm 1 produces output X with a cost function C_1(X)=\frac{X^2}{200}. Firm 2 produces output Y with a cost function C_2(X,Y)=\frac{Y^2}{100}-2X. Both firms face competitive markets. The competitive price of X is 6 and the competitive price of Y is \$ 5. There is no entry or exit into this market. What is the socially optimal production of X?

Answer 1

800

Step-by-step explanation:

The objective here is to determine the socially optimal production of X.

For this to occur ; it is crucial that both firm must merge together.

Therefore; the Profit will be = Total revenue - Total Cost

From the question; the total revenue = 6X + 5Y ; &

The total cost is :
`(X^2)/(200) + (Y^2)/(100) - 2X`

Now: The profit =
`6X+5Y - (X^2)/(200)- (Y^2)/(100)-2X`

=
`8X+5Y - (X^2)/(200)- (Y^2)/(100)`

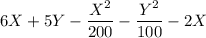
If the socially optimal production of X is the differential of the equation
`8X+5Y - (X^2)/(200)- (Y^2)/(100)`

(X) =
`8-(2X)/(200) =0`

=
`8-(X)/(100) =0`

=
`(X)/(100)=8`

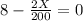
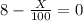
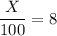
= 800

Thus the social optimal production of X = 800