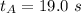Question

Constant Acceleration Kinematics: Car A is traveling at 22.0 m/s and car B at 29.0 m/s. Car A is 300 m behind car B when the driver of car A accelerates his car with a uniform forward acceleration of 2.40 m/s2. How long after car A begins to accelerate does it take car A to overtake car B?

Answer 1

The taken is
`t_A = 19.0 \ s`

Step-by-step explanation:

Frm the question we are told that

The speed of car A is
`v_A = 22 \ m/s`

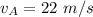
The speed of car B is
`v_B = 29.0 \ m/s`

The distance of car B from A is
`d = 300 \ m`

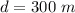
The acceleration of car A is
`a_A = 2.40 \ m/s^2`

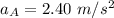
For A to overtake B

The distance traveled by car B = The distance traveled by car A - 300m

Now the this distance traveled by car B before it is overtaken by A is

`d = v_B * t_A`

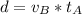
Where
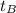`t_B` is the time taken by car B

Now this can also be represented as using equation of motion as

`d = v_A t_A + (1)/(2)a_A t_A^2 - 300`

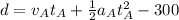
Now substituting values

`d = 22t_A + (1)/(2) (2.40)^2 t_A^2 - 300`

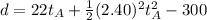
Equating the both d

`v_B * t_A = 22t_A + (1)/(2) (2.40)^2 t_A^2 - 300`

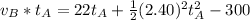
substituting values

`29 * t_A = 22t_A + (1)/(2) (2.40)^2 t_A^2 - 300`

`7 t_A = (1)/(2) (2.40)^2 t_A^2 - 300`

`7 t_A =1.2 t_A^2 - 300`

`1.2 t_A^2 - 7 t_A - 300 = 0`

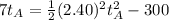
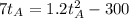
Solving this using quadratic formula we have that

`t_A = 19.0 \ s`