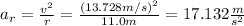Question

An astronaut is being tested in a centrifuge. The centrifuge has a radius of 11.0 m and, in starting, rotates according to θ = 0.260t2, where t is in seconds and θ is in radians. When t = 2.40 s, what are the magnitudes of the astronaut's (a) angular velocity, (b) linear velocity, (c) tangential acceleration, and (d) radial acceleration?

Answer 1

a) 1.248 rad/s

b) 13.728 m/s

c) 0.52 rad/s^2

d) 17.132m/s^2

Step-by-step explanation:

You have that the angles described by a astronaut is given by:

`\theta=0.260t^2`

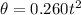
(a) To find the angular velocity of the astronaut you use the derivative og the angle respect to time:

`\omega=(d\theta)/(dt)=(d)/(dt)[0.260t^2]=0.52t`

Then, you evaluate for t=2.40 s:

`\omega=0.52(2.40)=1.248(rad)/(s)`

(b) The linear velocity is calculated by using the following formula:

`v=\omega r`

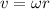
r: radius if the trajectory of the astronaut = 11.0m

You replace r and w and obtain:

`v=(1.248(rad)/(s))(11.0m)=13.728(m)/(s)`

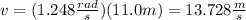
(c) The tangential acceleration is:

`a_T=\alpha r\\\\\alpha=(\omega^2)/(2\theta)=((1.248rad/s)^2)/(2(0.260(2.40s)^2))=0.52(rad)/(s^2)`

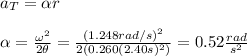
(d) The radial acceleration is:

`a_r=(v^2)/(r)=((13.728m/s)^2)/(11.0m)=17.132(m)/(s^2)`