Question

Determine the drag on a small circular disk of 0.02-ft diameter moving 0.01 ft/s through oil with a specific gravity of 0.89 and a viscosity 10000 times that of water. The disk is oriented normal to the upstream velocity. By what percent is the drag reduced if the disk is oriented parallel to the flow?

Answer 1

33.3%

Step-by-step explanation:

Given that:

specific gravity (SG) = 0.89

Diameter (D) = 0.01 ft/s

Density of oil
`\rho= SG\rho _(h20) = 0.89 * 1.94=1.7266(sl)/(ft^3)`

Since the viscosity 10000 times that of water, The reynold number
`R_E=(\rho VD)/(\mu) =(1.7266*0.01*0.01)/(0.234)=7.38*10^(-4)`

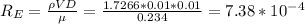
Since RE < 1, the drag coefficient for normal flow is given as:
`C_(D1)=(24.4)/(R_E)= (20.4)/(7.38*10^(-4))=2.76*10^4`

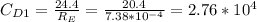
the drag coefficient for parallel flow is given as:
`C_(D2)=(13.6)/(R_E)= (13.6)/(7.38*10^(-4))=1.84*10^4`

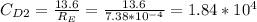
Percent reduced =
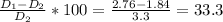`(D_1-D_2)/(D_2) *100=(2.76-1.84)/(3.3)=33.3` = 33.3%