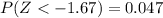Question

Owners of a minor league baseball team believe that a Normal model is useful in projecting the number of fans who will attend home games. They use a mean of 8500 fans and a standard deviation of 1500 fans. Using this model, answer these questions. a. Sketch and clearly label this Normal model, based on the 68-95-99.7 Rule. b. What proportion of the home games will have fewer than 6000 fans in attendance

Answer 1

a)
`\mu -\sigma = 8500 -1500 = 7000`

`\mu +\sigma = 8500 +1500 =10000`

`\mu -2*\sigma = 8500 -2*1500 = 5500`

`\mu +2*\sigma = 8500 +2*1500 =11500`

`\mu -3*\sigma = 8500 -3*1500 = 4000`

`\mu +3*\sigma = 8500 +3*1500 =13000`

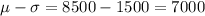
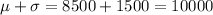
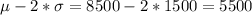
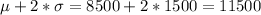
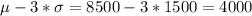
On the figure attached we have the illustration for required showing the percentages and the limits for each case

b)
`z= (6000-8500)/(1500)= -1.67`

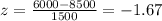
And using the normal standard table or excel we got:

`P(Z<-1.67) = 0.047`

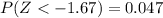
Explanation:

For this case we have the following properties:

`\mu = 8500, \sigma = 1500`

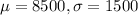
Part a

And for this case from the empirical rule we know that within one deviation from the mean we have 68% of the values , within two deviation 95% and within 3 deviations 99.7%. So then we can find the limits like this:

`\mu -\sigma = 8500 -1500 = 7000`

`\mu +\sigma = 8500 +1500 =10000`

`\mu -2*\sigma = 8500 -2*1500 = 5500`

`\mu +2*\sigma = 8500 +2*1500 =11500`

`\mu -3*\sigma = 8500 -3*1500 = 4000`

`\mu +3*\sigma = 8500 +3*1500 =13000`

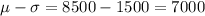
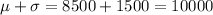
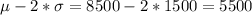
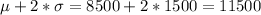
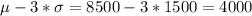
On the figure attached we have the illustration for required showing the percentages and the limits for each case

Part b

For this case we want to find this probability:

`P(X<6000)`

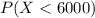
We can calculate the number of deviation below the mean with the z score formula given by:

`z = (X -\mu)/(\sigma)`

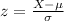
And replacing we got:

`z= (6000-8500)/(1500)= -1.67`

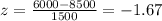
And using the normal standard table or excel we got:

`P(Z<-1.67) = 0.047`