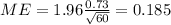Answer:

The critical value can be founded in the normal standard distribution table using the value of
 and we got
and we got
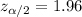 . Replacing the info given we got:
. Replacing the info given we got:
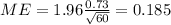
Explanation:
For this case we have the following info given:
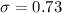 represent the population deviation
represent the population deviation
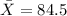 represent the sample mean
represent the sample mean
 represent the sample size
represent the sample size
And we want to find the margin of error for a confidence level of 95%. So then the significance level would be
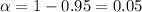 and
and
 . The margin of error is given by:
. The margin of error is given by:

The critical value can be founded in the normal standard distribution table using the value of
 and we got
and we got
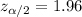 . Replacing the info given we got:
. Replacing the info given we got: