Question

Question 1 (1 point)

What is the area of the SHADED sector of the circle?
162° H
O a
Ob
Oc
400 x units2
20 x units2
180 x units2
40.x units2
od​

Answer 1

Question:

What is the area of the SHADED sector of the circle?

Image of the circle is attached.

A) 400π units²

B) 20π units²

C) 180π units²

D) 40π units²

Answer:

C) 180π units²

Explanation:

From thr circle, we can see that the given radius is 20 and the shaded part is 162°

The formula to calculate the area of the shaded sector of a circle is =

Area of the circle * fraction of the shaded part of the circle.

We know area of a circle = πr²

Therefore, area of the shaded sector =

`= \pi r^2 * (162)/(360)`

`= 20^2 * \pi * 0.45`

`= 400 * 0.45 * \pi`

`= 180 \pi`

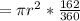
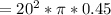
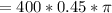
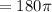
Area of the shaded sector of the circle is 180π units²