Question

In a random sample of 28 ​people, the mean commute time to work was 31.7 minutes and the standard deviation was 7.2 minutes. Assume the population is normally distributed and use a​ t-distribution to construct a 80​% confidence interval for the population mean mu. What is the margin of error of mu​? Interpret the results.

Answer 1

a)The 80% of confidence interval for the Population 'μ' is

(29.9121 ,33.4879)

b) Margin of error of mean ' 'μ' is = 1.7879

Explanation:

step(i):-

Given random sample 'n' =28

The mean of the sample x⁻ =31.7 min

The standard deviation of the sample's' =7.2

Step(ii):-

80% of confidence intervals:

The 80% of confidence interval for the Population 'μ' is determined by

`(x^(-) - t_{(\alpha )/(2) } (s)/(√(n) ) , x^(-) + t_{(\alpha )/(2) } (s)/(√(n) ) )`

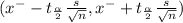
Degrees of freedom

γ = n-1 = 28-1 =27

`t_{(\alpha )/(2) } = t_{(0.20)/(2) } = t_(0.1) = 1.314`

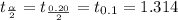
The 80% of confidence interval for the Population 'μ' is determined by

`(x^(-) - t_{(\alpha )/(2) } (s)/(√(n) ) , x^(-) + t_{(\alpha )/(2) } (s)/(√(n) ) )`

`(31.7-1.314 X (7.2)/(√(28) ) , 31.7+1.314 X(7.2)/(√(28) ) )`

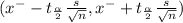
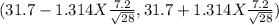
(31.7 -1.7879 , 31.7 +1.7879)

(29.9121 ,33.4879)

b)

Margin of error of mean is determined by

`M.E = {\frac{t_{(\alpha )/(2) } s}{√(n) } }`

`M.E = {(1.314 X 7.2)/(√(28) ) }`

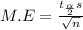
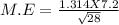
Margin of error =1.7879